When I was first presented with Fourier series, I mostly viewed them as a bunch of mathematical tricks to calculate a bunch of coefficients. I didn’t have a great idea about why we were calculating these coefficients, or why it was nice to always have these sine and cosine functions. It wasn’t until later that I realized that I could apply much of the intuition I had for vectors to Fourier series. This post will be the first in a series of three that develop this intuition:
- Part 1: Developing tools from vectors
- Part 2: Using these tools for Fourier series
- Part 3: A few examples using these tools
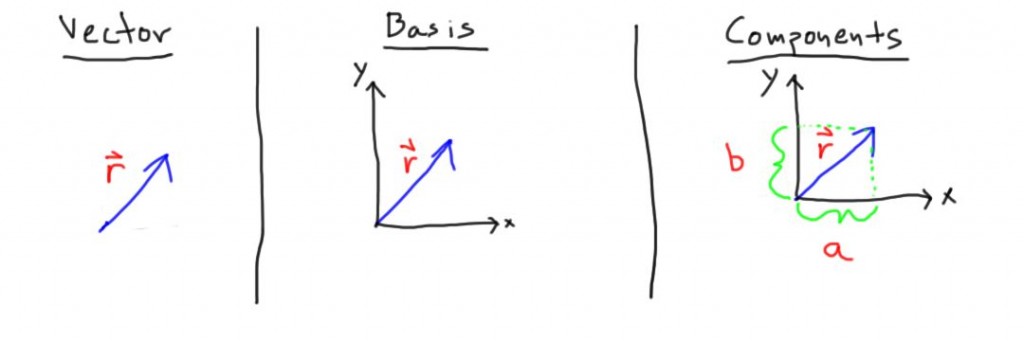
We can start with the abstract notion of a vector. We can think about a vectors as just an arrow that points in some direction with some length. This is a nice geometrical picture of a vectors, but it is difficult to use a picture to do a calculation. We want to turn our geometrical picture into the usual algebraic picture of vectors.
\(\vec r=a\hat x+b\hat y\)
Choosing a Basis
We will need to develop some tools to do this. One tool we will need is a basis. In our algebraic picture, choosing a basis means that we choose to describe our vector, \(\vec r\), in terms of the components in the \(\hat x\) and \(\hat y\) direction. As usual, we need our basis vectors to be linearly independent, have unit length, and we need one basis vector per dimension (they span the space).
Projection Operators
Now the question becomes: how can we calculate the components in the different directions? The way we learn to do this with vectors is by projection. So, we need projection operators. Things that eat our vector, \(\vec r\), and spit out the components in the \(\hat x\) and \(\hat y\) directions. For the example vector above, this would be:
\(\begin{aligned}\text{Proj}_x(\vec r)&=a,\\\text{Proj}_y(\vec r)&=b.\end{aligned}\)
We want these projection operators to have a few properties, and as long as they have these properties, any operator we can cook up will work. We want the projection operator in the \(x\) direction to only pick out the \(x\) component of our vector. If there is an \(x\) component, the projection operator should return it, and if there is no \(x\) component, it should return zero.
Great! Because we have used vectors before, we know that the projection operators are dot products with the unit vectors.
\(\begin{aligned}\text{Proj}_x(\vec r) &= \hat x\cdot\vec r=a\\\text{Proj}_y(\vec r) &= \hat y\cdot\vec r = b\end{aligned}\)
We can also check that these projection operators satisfy the properties that we wanted our operators to have.
So, now we have a way to take some arbitrary vector—maybe it was given to us in magnitude and angle form—and break it into components for our chosen basis.
Vector Rebuilder
The last tool we want is a way of taking our components and rebuilding our vector in our chosen basis. I don’t know of a mathematical name for this, so I’m going to call it a vector rebuilder. We know how to do this with our basis unit vectors:
\(\vec r = a\hat x+b\hat y = \text{Proj}_x(\vec r) \hat x+\text{Proj}_y(\vec r)\hat y = \sum_{e=x,y}\text{Proj}_e(\vec r)\hat e.\)
So, to recap, we have developed three tools:
- Basis: chosen set of unit vectors that allow us to describe any vector as a unique linear combination of them.
- Projection Operators: set of operators that allow us to calculate the components of a vector along any basis vector.
- Vector Rebuilder: expression that gives us our vector in terms of our basis and projection operators.
This may seem silly or overly pedantic, but during Part 2, I’ll (hopefully) make it clear how we can develop these same tools for Fourier analysis and use them to gain some intuition for the goals and techniques used.
Youtube companion to this post: