Do we in the US still have the same Senate as it existed in 1790 (first census)? I’ll attempt to answer this question with regards to one particular attribute: the division of senators by percentiles of the population. Unlike the House, the Senate is not meant to represent states proportional to their population; each state gets 2 senators. When this system was created, the states had some distribution of large and small populations. Over time, the number of states and their populations have changed.
When the Senate was created, it was known that it would represent states but not individuals equally. This might be a reasonable system if the states’ populations are not too skewed [1]. It does become an obviously ridiculous system in the skewed limit. If a state lost enough residents such that its population became 2, it would be pretty bizarre to have them both as senators and have one senator represent one person’s vote. How skewed are we and has this changed since the late 1700s?
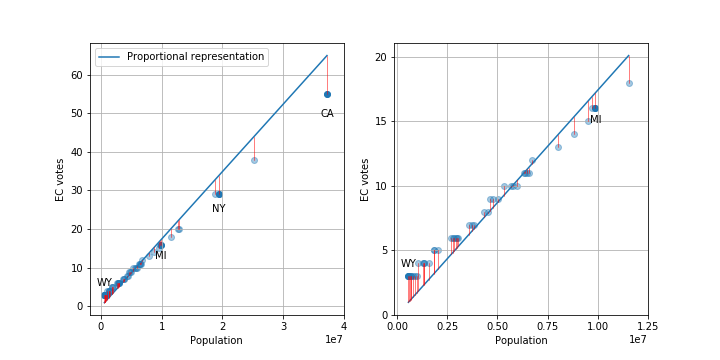
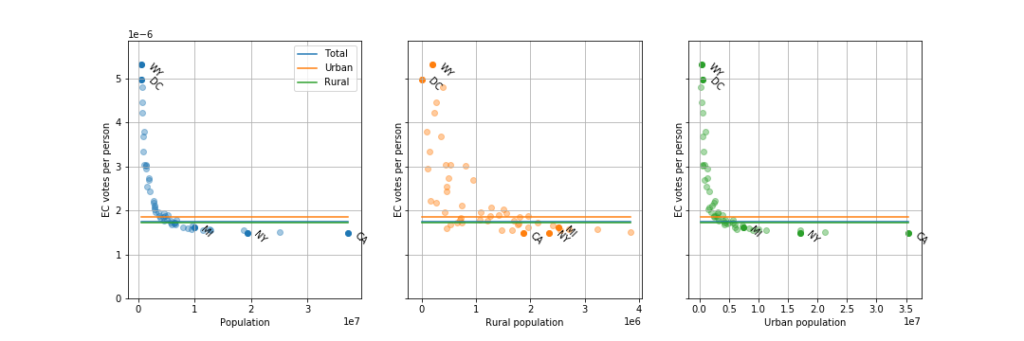
A simple way of answering this question is to break the US’s population into percentiles by how many senate votes they have. We’ll do this for four percentiles: 0-25%, 25-50%, 50-75%, and 75-100%. 0-25% percentile is the 25% percent of the population which has the largest fraction of a Senate vote, i.e. the 25% of the US population from the states with the smallest populations. This same process applies for the next 3 percentiles. If we know the population of the states [2] over time (available through the census), we can calculate the percentiles.
What does this look like for the 1790 through 2010 censuses?
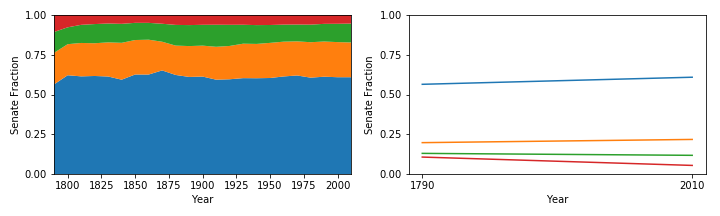
The large blue area is the fraction of Senate seats going to the top 25% of the population (most Senate representation). It has hovered just over 60% of the Senate vote and has increased about 4% from 1790 to 2010 (much of that happened in the first decade).
The next orange and green areas show the next two percentiles which have increased by 2% and decreased by 1% respectively.
The small red area is the fraction of Senate seats going to the bottom 25% of the population (least Senate representation). It has hovered around 5% of the Senate vote and has decreased about 4% from 1790 to 2010 (much of that happened in the first decade).
This means that the top and bottom 25%s of the country currently have a 10x disparity in Senate representation.
And over time, the 50% of people who live in the smallest states, i.e. have the most Senate representation, have about 6% more voting power (equivalent to 6 more senators) in the Senate compared to 1790. Conversely, the 50% of people who live in the largest states, i.e. have the least Senate representation, have lost about 6% (lost 6 senators). I’ve rounded to whole numbers, so things don’t exactly add up as I’ve presented.
Recent trends
These percentiles move around a lot in the first 100 years of the US and those trends probably are not still happening today. What about if we look at the last 50 years?
In the last 50 years, the 50% of the population with the most representation in the Senate (smallest states) have had no significant change in representation. The 25% of the population with the least Senate representation have lost about .2% of a Senate seat per decade and the 25% with the second least representation have gained about .3% of a Senate seat per decade.
So the two main conclusions are one: that there is a large degree of skewness (~10x) in Senate representation, and two: that this has been relatively stable except for the 25% of the population with the least Senate representation (largest states) which has lost about half of its representation since 1790.
Notes
[1] I’m not commenting here on whether having the Senate as a congressional body is or was a good idea, just whether that body has changed over time in this particular way.
[2] I’ve removed the enslaved population in states since they had no representation.
Code to reproduce these plots (and more!) can be found here.